Experiment with colours and proportion
Top-Slider
vertical proportion adjustment
Bottom-Slider
horizontal proportion adjustment
Buttons C1..C4
repeatedly click to change colors 1 to 4
Buttons Min / Max
show minimum or maximum number of modules
Buttons - / +
half or double number of modules
In blelbspot 01, you can allocate to every colour field 6 different shades of grey including black and white or 6 different primary colours. The cross-hairs can be moved on the right-hand diagram to alter the proportions of the four fields of a square picture module. Counting the various zoom levels, billions of different images can be created using this tool. The exceptional features of some of these images are commented on below :
Even with grey tones, interesting phenomena can be observed. In perception research, we talk of the transparency effect (1) which can be systematically examined by means of patterns of stripes. If we choose four different shades of grey for the four elements, 24 different configurations become possible. In the case of 8 configurations, we can say precisely which stripes appear to run at the front of the picture and which are located, partially covered, in the middle-ground. In pictures 1 and 2, perception of transparency is unambiguous.
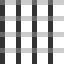
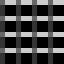
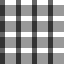

In the case of 8 further configurations, we can speak of ambiguous transparency, that is to say, as in picture 3, there are two possible interpretations which are not perceived with the same degree of ease.
In the case of the remaining 8 configurations, no transparency is evident; there are no fields which allow a background to shimmer through. Although we can see horizontal and vertical stripes, the elements at the intersections are opaque like the black squares in picture 4.
The geometry of the stripes, which can be changed in blelbspot 01 by moving the crosshairs, has no influence on these different categories. Research findings relating to the conditions governing transparency can be found in various works including those of Metelli (2).
Fabio Metelli (2) developed a theory about how the properties of the elements are split up in the transparency range. This only applies very roughly in the experiments shown here. According to Metelli, the colour properties of overlapping are governed by the proportional addition of colour from the properties of the foreground and the opaque middle-ground. Metelli determines the hypothetical degree of mixing algebraically from the light values of the individual colour fields. We believe that the blue, green and red content of the individual mixed colours should be investigated separately and how they work together in the transparency range explored. In addition to that, it has been shown that the shape and the structural organisation of the elements play a role. It is also necessary to take the Retinex Theory of Edwin H. Land (3) into account. In any case, the following colour illusion already shows that Metelli's assumption cannot be valid in all situations.

If we apply the theory of transparency to the grey values of the colours used in pictures 5 - 8, a pattern of stripes demonstrating ambiguous transparency is produced. It is possible to see either the vertical stripes in cyan or the horizontal ones in red in the foreground. In contrast to the grey value rules, however, we can force light horizontal or vertical stripes into the foreground. The use of colours increases the complexity of the perceptual experience.
The neutral grey squares appear to have a reddish hue.



Pictures 6 through 8 demonstrate a constant doubling of scale. It becomes increasingly difficult to identify the borders of the structures as straight equidistant lines. The geometrical/optical illusions change. All neighbouring fields have an influence on one another. If we observe picture 8 from a greater distance, it soon becomes possible to see an integral grey value which can be predicted using the rules of proportional colour addition.
Picture 9 shows narrow horizontal stripes in the foreground which are strongly influenced by their larger neighbouring elements. When looked at from close up, the grey fields demonstrate an intensive red hue; when looked at from further away, however, the grey appears bluish. When we see black as the background, the red columns appear in the middle-ground and as a result of the horizontal stripes in front of them demonstrate rhythmical colour distortions and constriction. When we see red as the background, the black columns in the middle-ground demonstrate concave distortion. With black in the middle-ground, there is no colour distortion.

The geometrical illusion, which jumps from the red objects to the black ones when background and middle-ground are interchanged, can be better understood in the light of the findings of Gaetano Kanizsa (5). Kanizsa shows that when one colour is positioned over another, the border always belongs to the object in front. Picture 9 shows for the first time that with spatial organisation that can be interpreted in various ways an illusion of the border can also tilt; the aforementioned border distortion changes the sign.

Picture 10 shows white or black columns with distorted borders in the middle-ground and opaque red stripes in the foreground which appear light red over the black and dark red over the white. This colour illusion is a special case of simultaneous contrast.

What can be seen here are either vertical white stripes with blue inclusions in the foreground or horizontal blue stripes in the background. What is striking here is the size illusion; the group of white stripes seems wider than the group of blue stripes. Light objects on a black background appear to expand, while dark objects on a light background appear to shrink.

According to Metelli's theory the narrow horizontal stripes should appear to be transparent. In fact, they appear to be opaque. In this picture, the spatial organisation has four possible interpretations; the vertical yellow bands or the vertical white ones can be in the foreground, or alternatively the horizontal black stripes or horizontal yellow bands are experienced at the front. In the first case, the background seems white, in the second yellow, in the third yellow and in the fourth black. The border illusions follow these changes; the horizontal black stripes seem wider than the vertical white ones.

Border illusions dominate in picture 13; the brain is not capable of seeing the borders of the vertical bands as straight lines. This distortion is caused by the black inclusions. The yellow rectangles tend to pull in and appear concave; the horizontal borders expand and bend out slightly, the black squares are distorted into knots. The bamboo effect can probably not be explained by the established size illusion.

This effect occurs when the colours used in the figures and the ground have approximately the same degree of lightness and are decoded by the colour receptors on the retina at different speeds. Blue objects on a red ground begin to dance when the light is dim, and when the picture is shaken slightly their geometry is registered by the retina out-of-phase. Sir Charles Wheatestone and Sir David Brewster published this effect in 1844. This phenomenon is known in art history under the name of "fluttering hearts" thanks to the work of Marcel Duchamp (7). In addition, angle distortion and wavy shaped configuration of the objects occur. If the figures and ground are exchanged, the geometry of the red grid in the foreground is stabilised.

In picture 15, the cyan line segments on the black grid seem to be surrounded by a soft fluorescent shimmer, which spreads out into the intermediate white spaces. This illusion was first discovered by the Dutch psychologist, van Tuijl in 1975 (6). In addition, the intermediate white spaces take on a greyish-reddish hue.

The optical effects at the intersections of a regular grid have been known since 1870. In the Hermann grid, light or dark points appear which are assumed to be an accompanying effect of neuronal image processing. The receptors triggered by the intersection points are subject to lateral inhibitions from four sides, while all the other points of the grid are affected from only two sides. In Picture 16, the intersection points are coloured white rather than the yellow of the classic Hermann grid. This leads to the occurrence of a new colour effect. Around the spot on which the eye is fixed, the intersections remain white. Away from this point they flash lilac; as the eye roves over the picture, the coloured areas move, too. When the distance from which the picture is viewed is increased, their number multiplies. Lateral inhibition is only removed in the area of the fovea centralis. Only those intersection points which are not in the fovea centralis area remain unaffected by the illusion.
Here, you can see two different pictures. Compare their features with regard to colour, shape and spatial layering. In fact, these two pictures are identical apart from having been rotated through 90 degrees. Both the colour and geometrical illusions probably stem from a preferred reading direction and from the slight astigmatism that virtually everybody has.


What is striking here is Wilhelm von Bezold's (4) colour illusion, which is also referred to as the assimilation effect, and which still remains a neurological puzzle today. Both pictures contain the same colours but their different positions relative to one another lead to extreme changes in colour. The same red is perceived as red-violet in one picture and as orange-red in the other. Blue and yellow change their hues less because - in this case - only two neighbouring elements are different. The results of an in-depth investigation of the Bezold effect together with a parameter study and effect optimisation have been published (8).

